Mutlak Değer ve Özellikleri

Matematik hayatımızın her yerinde karşımıza çıkmaktadır. Bugün ki ele alacağımız konuda matematikte en çok karşılaşılan konulardan biridir. Mutlak değer de bu konulardan biridir. Anlatıma geçmeden önce Mutlak değerin tanımını yapalım ki konuyu daha net anlamış olursunuz. Mutlak Değer; Bir gerçek sayının, sayı doğrusu üzerinde bulunduğu yerin sıfıra (yani başlangıç noktasına) uzaklığına o sayısının mutlak değeri denir. Gösterimi |a| şeklindedir. Hemen bir örnek ile açıklayalım.

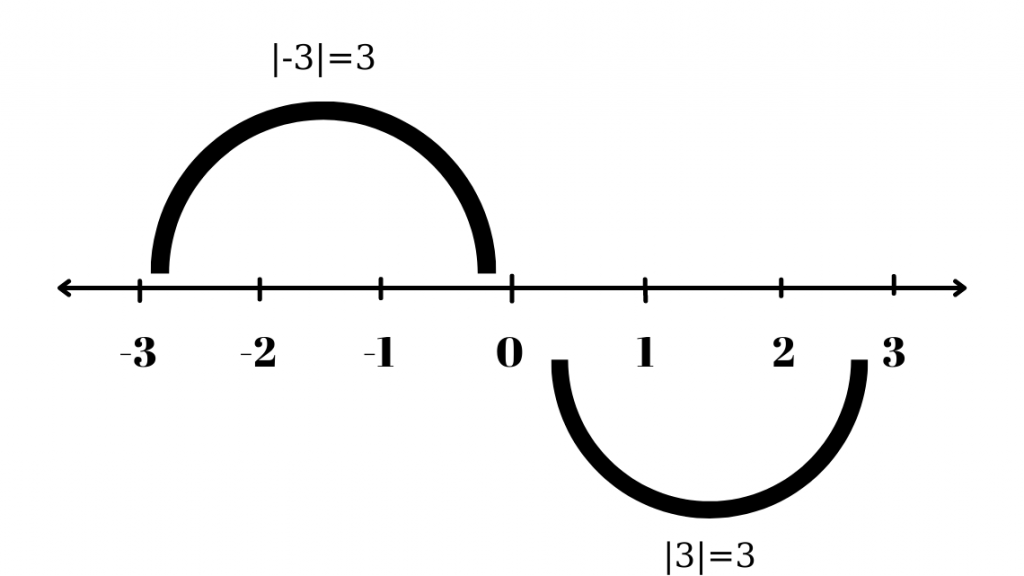
Örnek: 3 ve -3 sayısının 0’a olan uzaklığı 3 birimdir. Sembolle gösterimi |3| = 3, |-3| = 3 ‘tür.

Yukarıdaki örnekte de görüldüğü gibi sayısın 0’a uzaklığının sayısal değeri o sayısal değeri o sayının mutlak değerini gösterir.

Not: Mutlak değer x ∈ R olmak üzere;

1) X > 0 ise |X|= X
2) X < 0 ise |X|= -X
3) X=0 ise |X|= 0 olarak tanımlana bilir.

Dikkat Edilmesi Gerekenler

• Mutlak değerin içindeki sayı 0’dan küçük ise ( |-X| ), mutlak değerin dışına (-1) ile çarpılarak çıkartılır.

Yani; X < 0 ise |-X|.(-1)=X

Örnek: 2x < 0 ise mutlak değerini bulalım.

|-2x|.(-1)=2x ‘ dir.

• Mutlak değerin içindeki ifade 0’a eşit yada 0’dan büyük ise mutlak değerinin dışına olduğu gibi çıkmalıdır.

Yani; x>0 ise |+x|=x ‘dir.

Mutlak Değerin Özellikleri

a ve b x ∈ R olmak üzere; sıfıra

1)Gerçek bir sayının mutlak değeri eşit yada 0’dan büyüktür.

2)Gerçek iki sayının çarpım durumundaki mutlak değeri; bu iki sayısının mutlak değerinin çarpımına eşittir.

|a.b|=|a|.|b|

3)Gerçek iki sayısın bölme durumunda ki mutlak değeri, bu iki sayının mutlak değerinin bölümüne eşittir.

b≠0 => | a\b | = |a| \ |b|

4)Gerçek bir sayının pozitif tam sayı kuvvetinin mutlak değeri, mutlak değerinin aynı kuvvetine eşit olur.

N ∈ Z => |aⁿ|=|a| ⁿ

5) Gerçek olan iki sayının toplamının mutlak değeri sayıların ayrı ayrı mutlak değerlerinin toplamından küçük veya eşittir. Büyük olan sayının işaretine dikkat edilmelidir.

|a+b|≤|a|+|b|

Tam Sayılar, Pozitif ve Negatif Tam Sayılar hakkında da bilgi almak isterseniz linke tıklayabilirsiniz.